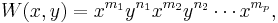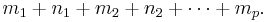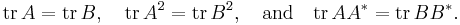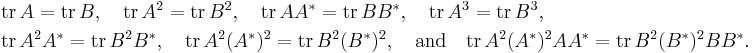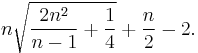Specht's theorem
In mathematics, Specht's theorem gives a necessary and sufficient condition for two matrices to be unitarily equivalent. It is named after Wilhelm Specht, who proved the theorem in 1940.[1]
Two matrices A and B are said to be unitarily equivalent if there exists a unitary matrix U such that B = U *AU.[2] Two matrices which are unitarily equivalent are also similar. Two similar matrices represent the same linear map, but with respect to a different basis; unitary equivalence corresponds to a change from an orthonormal basis to another orthonormal basis.
If A and B are unitarily equivalent, then tr AA* = tr BB*, where tr denotes the trace (in other words, the Frobenius norm is a unitary invariant). This follows from the cyclic invariance of the trace: if B = U *AU, then tr BB* = tr U *AUU *A*U = tr AUU *A*UU * = tr AA*, where the second equality is cyclic invariance.[3]
Thus, tr AA* = tr BB* is a necessary condition for unitary equivalence, but it is not sufficient. Specht's theorem gives infinitely many necessary conditions which together are also sufficient. The formulation of the theorem uses the following definition. A word in two variables, say x and y, is an expression of the form
where m1, n1, m2, n2, …, mp are non-negative integers. The degree of this word is
Specht's theorem: Two matrices A and B are unitarily equivalent if and only if tr W(A, A*) = tr W(B, B*) for all words W.[4]
The theorem gives an infinite number of trace identities, but it can be reduced to a finite subset. Let n denote the size of the matrices A and B. For the case n = 2, the following three conditions are sufficient:[5]
For n = 3, the following seven conditions are sufficient:
For general n, it suffices to show that tr W(A, A*) = tr W(B, B*) for all words of degree at most
It has been conjectured that this can be reduced to an expression linear in n.[8]
Notes
- ^ Specht (1940)
- ^ Horn & Johnson (1985), Definition 2.2.1
- ^ Horn & Johnson (1985), Theorem 2.2.2
- ^ Horn & Johnson (1985), Theorem 2.2.6
- ^ Horn & Johnson (1985), Theorem 2.2.8
- ^ Sibirskiǐ (1976), p. 260, quoted by Đoković & Johnson (2007)
- ^ Pappacena (1997), Theorem 4.3
- ^ Freedman, Gupta & Guralnick (1997), p. 160
References
- Đoković, Dragomir Ž.; Johnson, Charles R. (2007), "Unitarily achievable zero patterns and traces of words in A and A*", Linear Algebra and its Applications 421 (1): 63–68, doi:10.1016/j.laa.2006.03.002, ISSN 0024-3795.
- Freedman, Allen R.; Gupta, Ram Niwas; Guralnick, Robert M. (1997), "Shirshov's theorem and representations of semigroups", Pacific Journal of Mathematics 181 (3): 159–176, doi:10.2140/pjm.1997.181.159, ISSN 0030-8730, http://pjm.math.berkeley.edu/pjm/1997/181-3/p07.xhtml.
- Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6.
- Pappacena, Christopher J. (1997), "An upper bound for the length of a finite-dimensional algebra", Journal of Algebra 197 (2): 535–545, doi:10.1006/jabr.1997.7140, ISSN 0021-8693.
- Sibirskiǐ, K. S. (1976) (in Russian), Algebraic Invariants of Differential Equations and Matrices, Izdat. "Štiinca", Kishinev.
- Specht, Wilhelm (1940), "Zur Theorie der Matrizen. II", Jahresbericht der Deutschen Mathematiker-Vereinigung 50: 19–23, ISSN 0012-0456, http://gdz.sub.uni-goettingen.de/dms/load/toc/?PPN=PPN37721857X_0050&DMDID=dmdlog6.